1. 임상 진단 기준
2) 환자의 수집 및 검사유무 지정(Patient Recruitment and Assignmment)
▶ 어떤 검사법을 평가하는 연구를 설계할 때에는 이 검사로 환자의 질병상태에 대한 정보나 최종 건강결과가 달라질 때 이를 감지해 내기 위해 필요한 환자 수를 계산해야 한다. 이를 계산하려면 "통계적 유의성(statistical significant; α, p-value)"이나 "검정력(statistical power; 1-β)"에 대한 개념을 이해하고 있어야 한다.
▶ 일반적으로 관찰된 차이가 우연히 발생한 확률이 1/20 이하(p<0.05)일 경우에 "유의한 차이"가 있다고 말한다.
이 기준을 이용하면 실제로는 차이가 없는데도 우연히 유의한 차이가 있는 것으로 판정될 확률이 1/20이 된다. 이런 오류를 제 I종 오류(type I error) 또는 알파오류(α error)라고 한다.
알파오류 외에도 제 II종 오류(type II error) 또는 베타오류(β error)라고 하는 또 하나의 오류가 있다. 베타오류란 실제로는 차이가 있는데도 표본의 수가 너무 적어서 통계적으로 유의한 차이가 나타나지 않을 경우 생기는 오류를 말한다.
표본의 수는 베타오류를 범할 확률에 지대한 영향을 미치므로, 환자군을 세분하면 각 군의 표본수가 줄어 실제로 차이가 있는데도 이를 발견하지 못할 가능성이 높아진다. 따라서, 표본수를 추정할 때는 알파오류와 통계적 검정력, 각 군 자료의 변이의 크기를 나타내는 분산, 임상적으로 의미 있는 반응의 차이, 검정의 방법 등을 고려해야 한다. 표본수 추정에는 공식을 이용하는 방법과, 표본수표에서 얻는 방법 등이 있다.
3) 검사의 정보내용에 대한 평가
(1) 판정행렬(Decision Matrices)
▶ 검사를 시행한 후에는 검사결과를 평가하기 위해 다음과 같은 간단한 2X2 행렬을 만든다. 검사결과는 정상과 비정상의 2항으로 나누어 행으로 표시하고 질병상태는 있다와 없다의 2항으로 나누어 열로 표시한다. 이 행렬의 네항에는 해당 검사결과와 질병상태가 맞는 환자의 수(백분율이 아님)를 기입한다.
| 질병 | |||||
| 있음(D+) | 없음(D-) | ||||
| 검사 | (T+) |
A(TP) | B(FP) | A+B | |
(T-) |
C(FN) | D(TN) | C+D | ||
| A+C | B+D | ||||
- 검사결과가 양성(positive)이고 질병이 있는 경우는 진양성(true positive, TP)
- 검사결과가 양성인데 질병이 없는 경우는 위양성(false positive, FP)
- 검사결과가 음성(negative)이고 질병이 없는 경우는 진음성(true negative, TN)
- 검사결과가 음성인데 질병이 있는 경우는 위음성(false negative, FN)
▶ 이 간단한 행렬로부터 다음과 같이 7개의 지표(ratio)가 구해지는데 이들은 검사의 정보내용을 반영한다.
정확도(Accuracy) = (A+D)/(A+B+C+D) = (TP+TN)/(TP+FP+FN+TN) |
▶ 예민도(sensitivity), 특이도(specificity)
- 예민도(sensitivity)
: 예민도는 진양성결과수를 질병이 있는 총 환자수로 나눈 값이며[A/(A+C)] 진양성율(true positive ratio, TPR)이라고도 한다.
검사의 예민도는 질병이 있는 환자만 검사해도 구해지며 질병이 없는 환자의 검사결과에 대해서는 아무것도 알려주지 않는다. 따라서 예민도는 단독으로는 정상과 질병상태를 구분하는 검사의 능력을 반영하지 못한다.
- 특이도(specificity)
: 특이도는 진음성결과수를 질병이 없는 총 환자수로 나눈 값이며[D/(B+D)] 진음성율이라고도 한다.
검사의 특이도는 예민도와 마찬가지로 단독으로는 정상과 질병상태를 구분하는 검사의 능력을 반영하지 못한다.
- 예민도와 특이도 중에서 어느 지표가 더 중요한가는 상황에 따라 그리고 양성 또는 음성 검사결과가 가져오는 영향에 따라 다르다. 일반적으로 효과적인 치료가 있고 질병이 중하여 진단을 놓치면 대가가 큰 질병에는 예민한 검사가 좋으며 진단되어도 건강결과를 크게 바꾸기 어렵고 위양성으로 판정하면 부담이 큰 치료를 받게 만들 때에는 특이도가 높은 검사가 좋다.
▶ 검사의 우도비(likelihood ratio)
- 양성검사의 우도비(likelihood ratio of positive test; L+)
: 양성검사의 우도비는 진양성율(예민도)을 위양성율(1-특이도)로 나눈 값이다. 양성검사의 우도비가 높을 수록 양성검사 결과가 질병이 있는 환자를 없는 환자와 식별하는 능력이 좋은 것이다.
- 음성검사의 우도비(likelihood ratio of negative test; L-)
: 음성검사의 우도비는 위음성율(1-예민도)을 진음성율(특이도)로 나눈 값이다. 음성검사의 우도비는 낮을수록 음성검사 결과가 질병이 없는 환자를 질병이 있는 환자를 구별하는 능력이 좋다.
▶ 6개의 지표는 질병의 유병률(prevalance, [(A+C)/(A+B+C+D)]에 무관하며 따라서 검사 자체의 특성을 반영한다.
언뜻 생각하면 진양성 결과수와 진음성 결과수의 합을 총 검사대상자수로 나눈 지표[(A+D)/(A+B+C+D)]가 검사의 정보내용을 반영하는데 있어서 가장 중요할 것 같다. 이 지표를 검사의 정확도(accuracy)라고 하는데 불행히도 이 지표는 질병의 유병률에 영향을 받으므로 검사의 정보내용을 잘 반영하지 못할 경우가 많다.
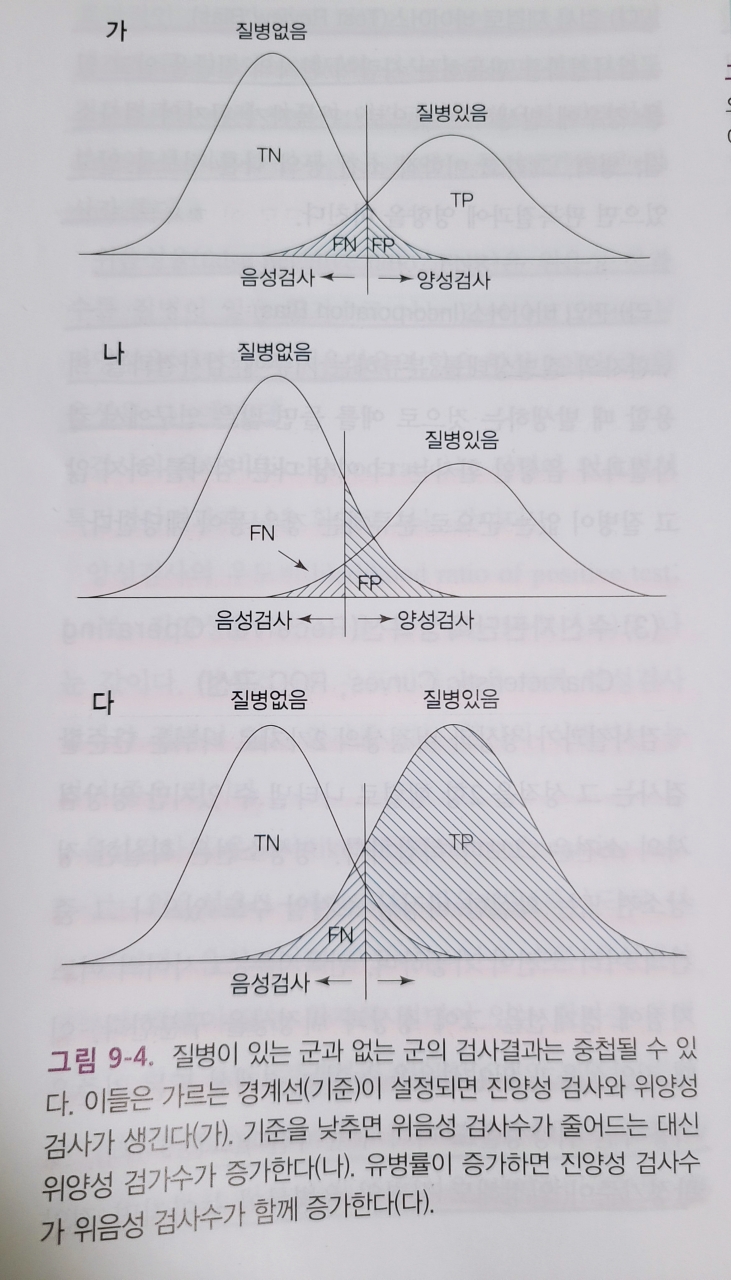
(3) 수신자판단특성곡선(Receiver Operating Charateristics Curves, ROC 곡선)
▶ 검사결고가 정상과 비정상의 2가지로 나뉘는 단순한 검사는 그 성적을 2항 행렬로 나타낼 수 있지만 영상검사의 소견은 그보다 복잡하다. 영상소견은 확실한 정상소견 또는 확실한 비정상 소견일 수도 있으나 그 중간의 여러 소견이 가능하며, 판독자는 그 사이의 어느 지점에 경계선을 그어 정상과 비정상을 구분한다. 이때 진양성율과 위양성율을 높이는 경계선 또는 기준을 이용하면 위양성율도 따라서 높아진다. 또 판정기준이 일정해도 질병의 유병률이 높아지면 진양성수와 위양성수가 증가한다.
2. 핵의학의 통계
1) 계측통계
(1) 계수(count)의 분포 및 변이계수
▶ 계측기로 원자핵의 붕괴에서 생기는 방사선을 계측할 때 그 계수는 Poisson 분포를 한다.
그러므로, 특정시간에 있어서의 계수를 N이라 하면, Poisson 분포의 성질에 따라 그 평균과 표준편차는 N±√N으로 표시할 수 있으며, 이의 변이계수(coefficient of variation, CV=표준편차/평균)는 √N/N = 1/√N로주어진다.
따라서, 계수 N은 1/(변이계수)^2이 됨을 알 수 있다.
한편, 실제의 계측에 있어서는 계수의 값이 충분히 크므로 Poisson 분포의 성질에 따라 정규분포로 간주하여도 무리가 없다.
(2) 계수율 및 신뢰 구간
▶ 분당계수율(cpm)이 주어졌을 때의 변이계수에 대해 알아보기 위해 t분간의 계측에서 N의 계수를 얻어 계수율 R = N/t 이 된 경우를 생각해 보자.
모집단에서 N은 Poisson 분포를 따르므로 그 모평균은 N, 모분산도 N 그리고 모표준편차는 √N이 된다. 따라서 R의 모평균은 N/t = R, 모분산은 Var(N/1) = 1/t^2, Var(N) = (N/t)^2 = R/t 로서 R±√(R/t)이 되며, 이때의 상대오차(혹은 변이계수)는 √(R/t)/R = 1/√Rt이 되어 결론적으로 같은 계수율 R을 얻는 경우 그 변이계수는 측정시간 t의 제곱근에 반비례하는 것을 알 수 있다.
예상문제
방사능의 계측에 있어 계측의 변이계수를 0.05 이하로 유지하려면 계수를 어떤 범위에서 얻어야 하는가?
(단, 배후 방사능 계수는 총계수의 1% 이상이 되지 않는다.)
변이계수 1/√N < 0.05, √N>1/(0.05)^2 = 400이 되므로 400 이상의 계수를 얻어야 한다.
(배후 방사능 계수가 총계수의 1% 이상이 되면 위의 식이 성립하지 않는다)
1분간 계측하여 100 count를 얻은 경우와 25분간 계측하여 2,500 count를 얻은 경우의 변이계수를 비교하여 보면 두 경우 계수율과 변이계수는 어떻게 되는가?
두 경우 모두 계수율이 100 cpm이나
전자의 경우의 변이계수는 1/√Rt1 = 1/√100x1 = 1/10,
후자의 경우의 변이계수는 1/√Rt2 = 1/√100x25 = 1/50로서
결국 변이계수가 1/5로 감소되었음을 알 수 있다.
'1교시. 의학 > 핵의학 : 고창순 핵의학 제4판' 카테고리의 다른 글
| 11 뇌종양 (0) | 2020.10.30 |
|---|---|
| 10 핵의학 진단 개론 - 1. 핵의학 영상법 개론 (0) | 2020.10.25 |
| 08 분자영상 - 1. 분자영상 개론, 3. 분자영상의 실제 (0) | 2020.10.15 |
| 07 방사선 생물학 - 2. 방사선 선량평가 (0) | 2020.10.14 |
| 06 방사성의약품 생산 및 품질관리 - 4. 방사성의약품 제조 및 품질관리 기준(GMP) (0) | 2020.10.12 |